S4 Tetrahedron
VISIT Tetrahedron. 4 points, 4 faces, 6 edges.
The Voronoi of a tetrahedron is a bigger tetrahedron (not shown)
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
Great, what next! READ about the website. LOOK at the Structures. BUY something special. DIG into the technical details. WHO wrote the website. SEE a Spherical Shell video. So cool!
When Bucky (Buckminster Fuller) and friends were in their prime, the available mathematical tools, especially for spherical coordinates, were primitive. For this reason, most of the classic geodesic dome material is about how to use simple math in order to cover a spherical surface originally defined with big triangles with littler triangles. This allowed shorter struts, and bigger spheres. Class I, Class II, and alternate breakdown are classic methods of subdividing one triangle into (easily computable) smaller triangles. Easy to see how the octahedron and icosahedron, which had more original triangles, became the fundamental starting spheres used at the time.
Times have changed. The omnipresent personal computer has incredible computing power.
The LGdome program made the illustrations in this book. LGdome searches for patterns on the surface of a sphere, limited by various constraints. Some of the patterns found are in the general published literature. Some are believed unique to this publication. Some are breakdowns of regular polyhedra. Some are not. The patterns are examined for useful properties aesthetics, ease of manufacture, ease of construction, strength of structure, and efficient use of available building materials being among them. Due to the strength of a geodesic roof, Shelter is safer. The shape means the Shelter receives less wind loading, and is quieter. Shelter includes houses, cabins, sheds, and greenhouses. The minimum material to build one allows easy transport to off-grid locations.
A pattern with few different elements is easier to make and build. Consider a hub. Each hub connects the correct number of struts in the correct order. Each strut connects to the hub with a bevel angle out of the sphere plane. Each strut has an internal angle separating it from the adjacent strut. The simplest construction would have those two angles the same for all struts. The tetrahedron, octahedron, cube, icosahedron, and dodecahedron have only have one strut length, and order is automatic. More complex hubs might have every strut, angle, and bevel different. Modern CNC machinery can manufacture the different hubs automatically, but keeping track of the different hubs, and struts during transport and construction is a chore.
Similar statements may be said of the faces, and struts. For this reason, those sphere patterns that are deemed too complex to build have arbitrarily not been included in the site. Contact the author if you have an interest in a pattern that was excluded.
Face sub-pattern groups can make it easier to build and assemble. The face GCD with the folding pattern offer clues to useful sub-patterns. Entire 6-face hubs are pre-assembled as hexagons and then attached as a unit. Various other breakdown sub-patterns allow the same utility. New breakdown patterns are shown for the tetrahedron, cube, and dodecahedron..
Planning to publish the folding patterns, and 3D-printed spheres. Also under consideration is full details of each component of a shape for manufacture or construction.
Spp names the basic spheres generated using Delaunay methods. pp is the number of points on the sphere. These spheres are composed of triangular faces. Vff names the Voronoi spheres generated from Delaunay spheres. ff is the number of faces on the sphere. Voronoi patterns tend to have 4-sided, 5-sided, and 6-sided faces. This may be augmented by a common name if known to the author. "S4" is a tetrahedron. "S12" is an icosahedron.
D may be appended to indicate 2v Class 1 (alternate) Method 1 breakdown. Similarly, DD indicates the 3v breakdown. S42D is the 2v-icosahedron pattern commonly used for small projects.
When new breakdowns are discovered within a pattern, -mm indicates the degree of breakdown, and it is often followed by the name of the original pattern.
The radius is chosen as 1.0 for Delaunay patterns and most use. Voronoi patterns circumscribe the sphere and touch the sphere at its center point. Thus have an edge point radius greater than 1.
A text file containing four tables which define the element geometry. Point table has the point coordinates in cartesian and spherical. Hub table has the geometry needed for hub construction. Face table has the face geometry. Edge table has the geometry needed to construct struts.
An OpenScad file to bring the shape into the 3D print world.
An .DXF file to show the faces, colors, and lines.
Many spheres were excluded by the Author for various reasons.
Email the Author if you want access to excluded material.
. Let P be the number of points on the sphere. When the sphere is evenly covered by triangles, the number of faces may be computed from
F = (P-2)*2
The number of edges may be computed from
E = (P-2)*3
This supports the notion that you must have three points to make 2 triangular faces (think both sides), which will then have three edges. Thus you can choose how many faces or edges you want, and then compute the number of points needed on the sphere.
Consider a sphere covered in triangles. A new point must go into the interior of one of the triangles. This new point would create 3 faces from the original face, thus adding 2 faces. The three new connecting edges, combine with the existing edges to define the new face sides. One new point gives 2 new triangles and 3 new edges.
Delaunay Spheres with more than 12 points tend to have 12 hubs with 5 spokes each. But they do not occur in the same spherical locations as in the icosahedron.
Both of these properties hold for spheres made totally of evenly distributed points gathered into delaunay triangles. But compare S22 with S22D, which shows an exception for triangulated spheres. Voronoi spheres are not covered in triangles, and are an exception.
This material generated from "Geodesic Domes" by Borin Van Loon. The book explains the concept rather well. I recommend it to anyone interested in the subject.
In a "Full 2V Triacon", One point is added at the centroid of each original face, and resulting total points can be collected, Delaunay-fashion, into a new set of faces.
A tetrahedron with 4 points and 4 faces would have 8 points and 12 faces. The result is a cube, with each face represented by two right triangles.
An S5 with 5 points and 6 faces would have 11 points and 20 faces..
An S6 with 6 points and 8 faces would have 14 points and 24 faces.
An S7 with 7 points and 10 faces would have 17 points and 30 faces..
An S_ with n points and (n-2)*2 faces would have 3n-4 points and 6n-12 faces.
Thus, if a delaunay sphere exists with n points with 8 or more points, there would be "full triacon" spheres with 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, 47, ...... points.
This section contains the patterns. It is organized from simple to complex, and ordered in increasing number of points on the sphere surface. The top and side view of most of the spheres is given, as well as the unfolded template. The template may be used to make a folding model out of stiff paper. It will reveal much about the relationship between the different faces. The coloring serves to identify the different face groups.
VISIT Tetrahedron. 4 points, 4 faces, 6 edges.
The Voronoi of a tetrahedron is a bigger tetrahedron (not shown)
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
VISIT Triangular bi-pyramid. 5 points, 6 Faces:@0.96825, 9 Edges in two groups: 6@1.41421, 3@1.73205
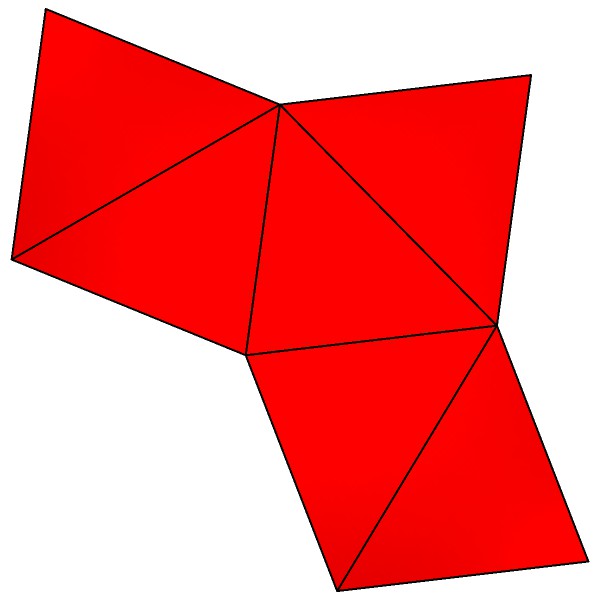 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
VISIT Triangular prism. 6 points, 5 Faces, 9 Edges in two groups: 6@1.41421, 3@1.73205
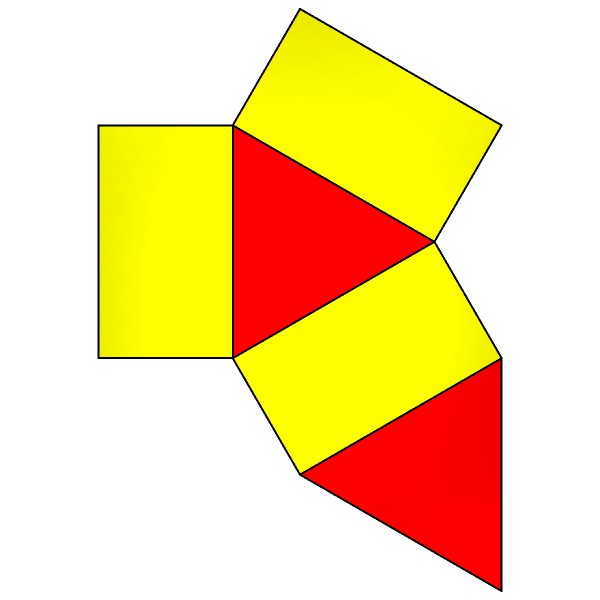 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
VISIT Octahedron. Also called a square bi-pyramid. 6 points, 8 Faces:, 12 Edges
 FLAT
FLAT
 ALL
ALL
VISIT Voronoi Cube. Points 8, Faces 6@area 4.00000, Edges 12@Length 2.00000
 FLAT
FLAT
 ALL
ALL
7 points, 10 Face Areas:@0.75605, 15 Edges in two groups: 5@1.17557, 10@1.41421
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
10 Points, 7 Face Areas in 2 groups: 5@2.90617, 2@3.63271, 15 Edge Lengths in 2 groups: 10@1.45309, 5@2.00000, Note two other patterns with 10 points.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
If all triangles - 8 Points, 12 Faces, and 18 Edges. But two pair of triangles form a square, in two cases. Thus reduced to 8 Points, 10 Faces in 2 groups: 8@0.67397, 2@1.36242(square), 16 Edges: 8@1.16722, 8@1.29391 Bottom has side view, folding template, and top view.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
10 Points, 8 Face Areas@2.52342, 16 Edge Lengths in 2 groups: 8@1.24486, 8@2.04149
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
9 Points, 14 Faces: 6@0.58736, 6@0.62668, 2@0.65699 21 Edges: 12@1.13527, 6@1.23176, 3@1.40605
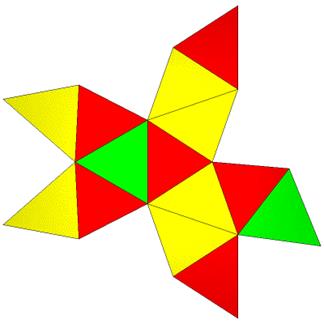 FLAT
FLAT
 LEFT
LEFT
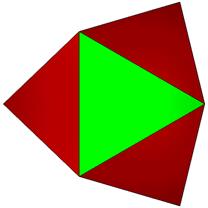 TOP
TOP
14 Points, 9 Face Areas in 2 groups: 3@1.91844, 6@2.17399 21 Edge Lengths in 3 groups: 3@0.68551, 6@1.12057, 12@1.39114.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
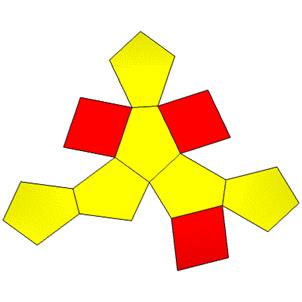
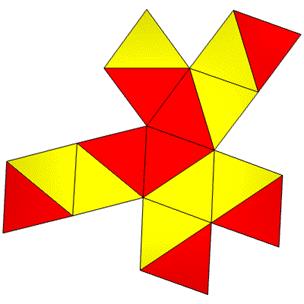
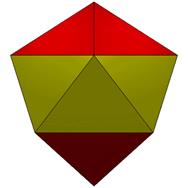
10 Points, 16 Face Areas in 2 groups: 8@0.55465, 8@0.56583, 24 Edge Lengths in 3 groups: 8@1.07658, 8@1.09061, 8@1.28310
 FLAT
FLAT
 LEFT
LEFT
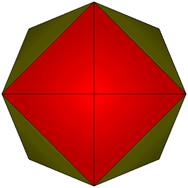 TOP
TOP
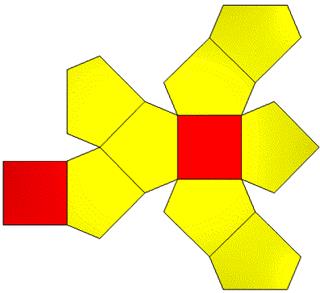
16 Points. 10 Face Areas in 2 groups: 2@1.63188, 8@1.83372. 24 Edge Lengths in 3 groups: 8@0.70774, 8@1.27743, 8@1.28165
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
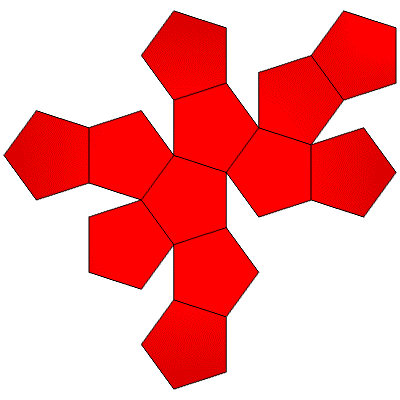
20 Points, 12 Face Areas@1.38757. 30 Edge Lengths@0.89805
The Voronoi dodecahedron differs from the Spherical dodecahedron. The Voronoi faces are tangent to the sphere at the face center. The Delaunay faces touch the sphere at the face points. Thus Voronoi dimensions are slightly bigger.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
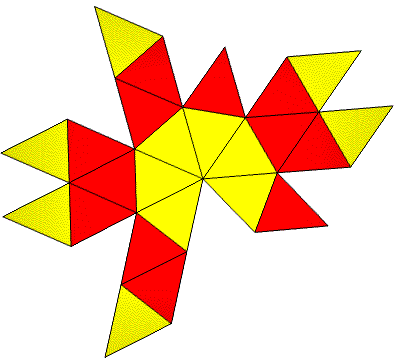
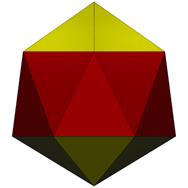
24 Faces in 2 groups: 12@0.41130, 12@0.41772. 36 Edges in 3 groups: 12@0.88836, 12@1.02700, 12@1.04005.
 FLAT
FLAT
 LEFT
LEFT
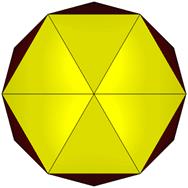 TOP
TOP
24 points. 14 Face Areas in 2 groups: 12@1.11904, 2@1.28400 36 Edge Lengths in 3 groups: 12@0.69845, 12@0.70300, 12@0.98245
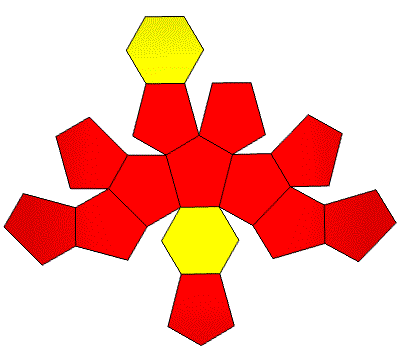 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
Hub 16 Points. 28 Faces: 4@0.34305, 12@0.36003, 12@0.38030. 42 Edges: 6@0.82982, 12@0.89008, 12@0.90559, 12@1.03859.
GCD is 4. 7 face tetra breakdown triangles are 1 red, 3 green, and one-half of 6 yellow.
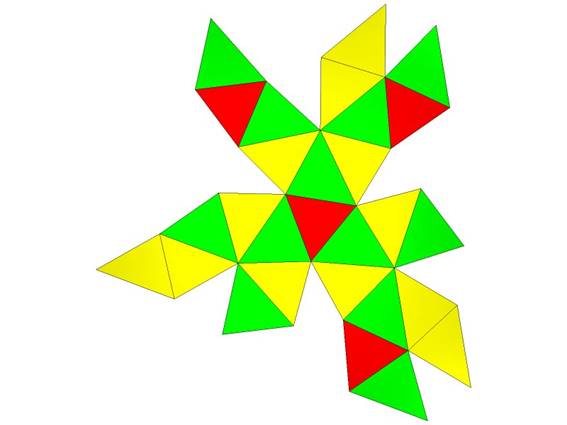 FLAT
FLAT
 LEFT
LEFT
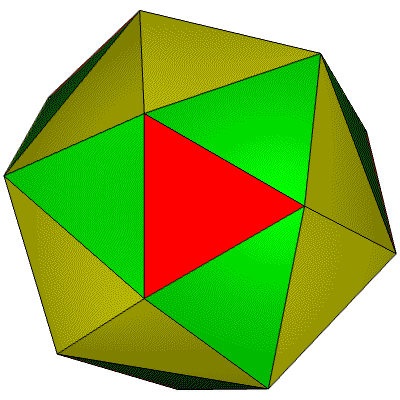 TOP
TOP
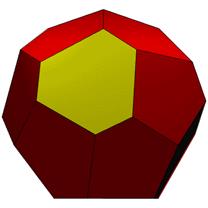
28 points. 16 Face Areas in 2 groups: 12@0.94008, 4@1.05230, 42 Edge Lengths in 4 groups: 12@0.47120, 12@0.76741, 12@0.81757, 6@0.91192,
GCD is 4. Tetra breakdown
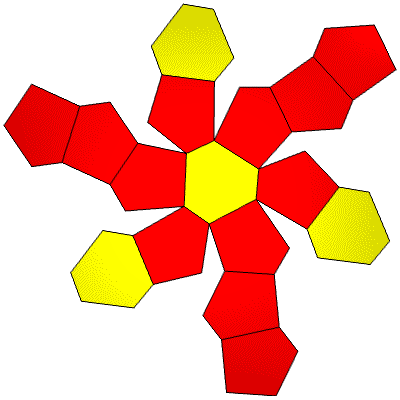 FLAT
FLAT
 TOP
TOP
 LEFT
LEFT
12 Hub5 and 4 Hub6. 30 Face Areas in 3 groups: 10@0.32912, 10@0.35142, 10@0.35729 45 Edge Lengths in 4 groups: 20@0.84557, 10@0.88580, 10@0.93361, 5@1.17557
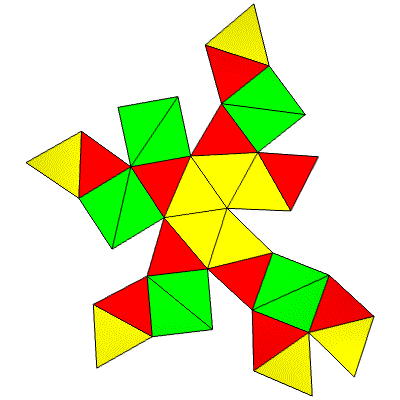 FLAT
FLAT
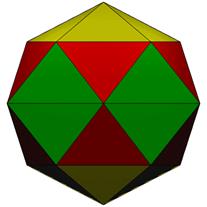 LEFT
LEFT
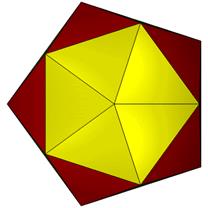 TOP
TOP
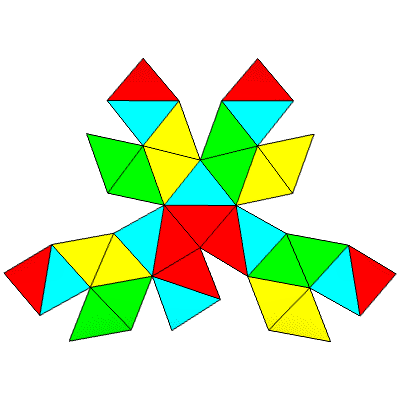
30 Hub3: 17 Face Areas in 3 groups: 2@0.88648, 5@0.89869, 10@0.90384: 45 Edge Lengths in 4 groups: 5@0.06034, 10@0.56668, 10@0.71781, 20@0.91615,
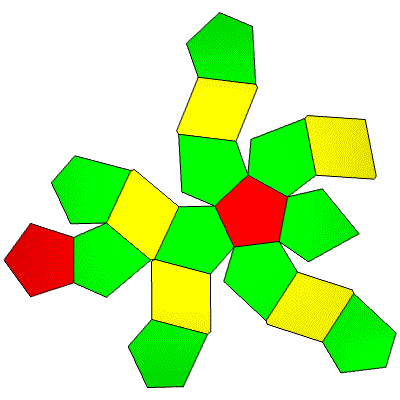 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
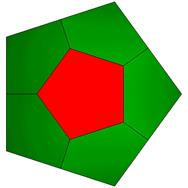
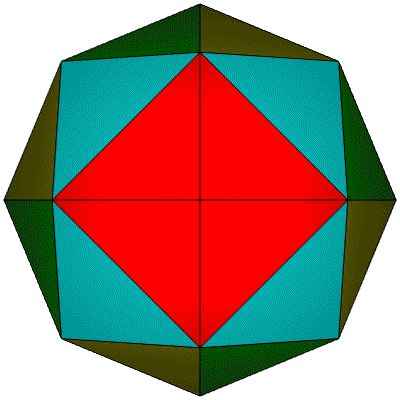
18 Hubs 2@4,8@5, 8@6: 32 Face Areas: 8@0.32026, 8@0.32540, 8@0.32540-rev, 8@0.34149: 48 Edges: 8@0.80568, 16@0.83714, 8@0.85510, 8@0.91417, 8@1.04286
Contrast to S18O 2vOctahedron, which also has 18 Points. Yes, there is more than one stable pattern for a set of points. Note the 4-part rotational symmetry. Face GCD 8 allows tetrahedron and octahedron breakdowns.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
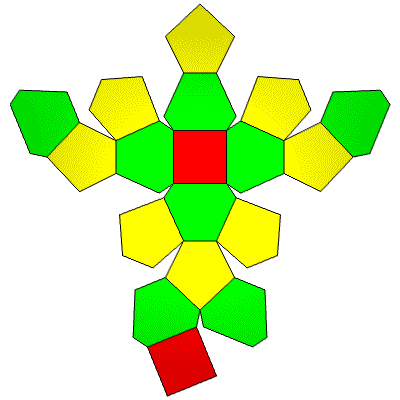
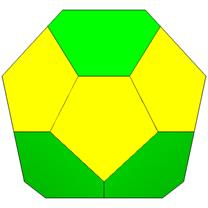
32 Hub3: 18 Face Areas in 3 groups: 2@0.77486, 8@0.82389, 8@0.87133: 48 Edge Lengths in 5 groups: 8@0.28461, 8@0.54470, 8@0.67701, 16@0.78911, 8@0.88023,
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
32 Faces in 2 groups: 24@0.28974, 8@0.43301: 48 Edges in 2 groups: 24@0.76537, 24@1.00000:
Formed by Classic 2v class 1 Method 1 breakdown of S6 Octahedron. Compared to the S18, This S18O has less variety of edges and faces, and flat dome equator. The S18 has smaller ranges of face area and edge length area, and so is more uniform, and stronger.
 FLAT
FLAT
 ALL
ALL
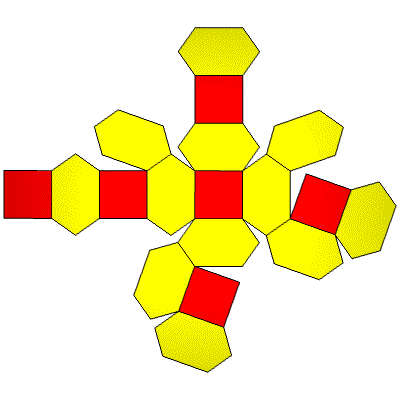
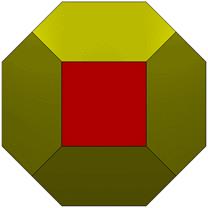
32 Hub3: 18 Face Areas in 2 groups: 6@0.68629, 12@0.92893: 48 Edge Lengths in 2 groups: 24@0.50730, 24@0.82843:
Voronoi of 2vOctahedron
 FLAT
FLAT
 ALL
ALL
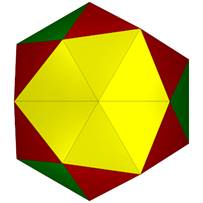
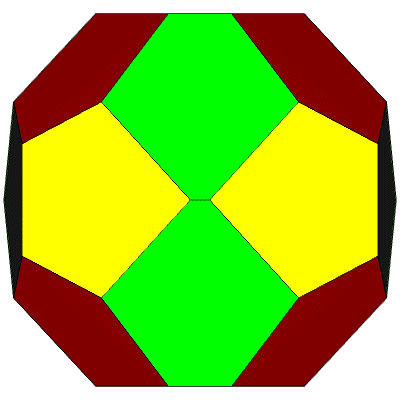
20 Hubs: 12@5, 8@6: 36 Faces in 4 groups: 12@0.28312, 12@0.30162, 6@0.30486, 6@0.30904: GCD is 6. 54 Edges in 7 groups: 6@0.77714, 12@0.78711, 12@0.80381,12@0.83735, 3@0.84256, 6@0.96213, 3@1.07431:
Three-part Rotational symmetry. Might work well in dome groups. The (blue) vertical triangles meet with a 5 degree bevel at their common edge.
 FLAT
FLAT
 TOP
TOP
 LEFT
LEFT
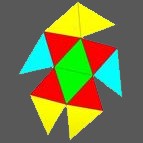
36 Hub3: 20 Face Areas in 4 groups: 6@0.71837, 6@0.73765, 6@0.75527, 2@0.77366: 54 Edge Lengths in 8 groups: 1@0.10378, 2@0.10390, 6@0.34025, 12@0.56679, 3@0.60297, 12@0.66649, 6@0.78028, 12@0.78553,
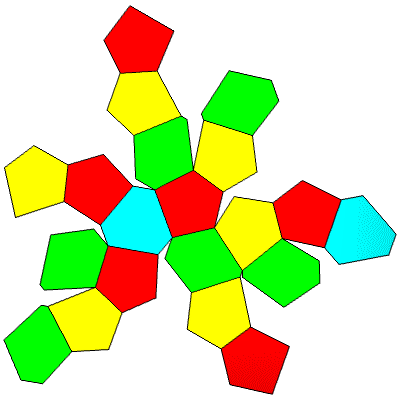 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
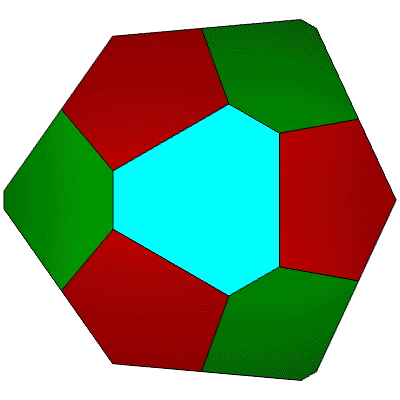
22 Hubs 12@5, 6@6, 4@6: 40 Face Areas in 4 groups: 12@0.26427, 4@0.27445, 12@0.27501R, 12@0.27501L: 60 Edge Lengths in 4 groups 12@0.73567, 24@0.77408, 12@0.79612, 12@0.91938.
10::1 Tetrahedron symmetry. Center blue triangle, surrounded by 3 red, 3 yellow, and 3 green triangles.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
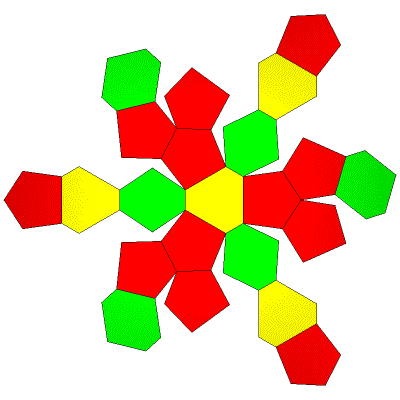
40 Hub3: 22 Face Areas in 3 groups: 12@0.64297, 4@0.68351, 6@0.68702: GCD = 2. 60 Edge Lengths in 4 groups: 12@0.31579, 12@0.54179, 24@0.62361, 12@0.73866:
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
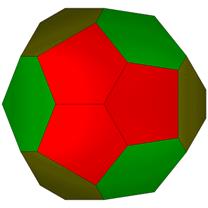
22 Hubs 5@4, 2@5, 15@6: 40 Face Areas in 3 groups: 20@0.23777, 10@0.26073, 10@0.34378: 60 Edge Lengths in 5 groups: 10@0.61803, 10@0.75569, 10@0.77503, 10@0.82251, 20@0.93162:
Class 1 method 1 breakdown from S7. The red and yellow triangles are mirrors of each other, together forming face group 1.
 FLAT
FLAT
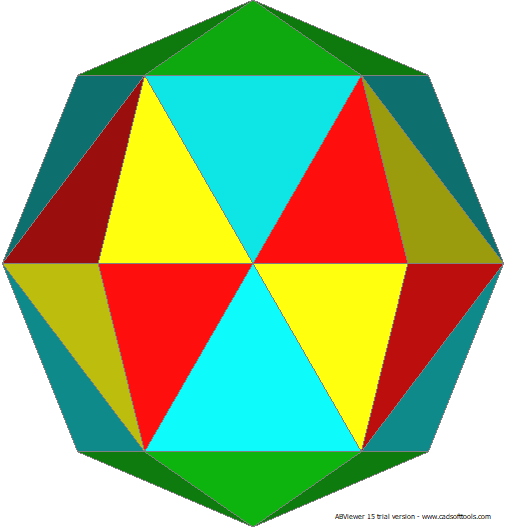 LEFT
LEFT
 TOP
TOP
40 Points. 22 Face Areas: 5 @ 0.54633, 2 @ 0.60500, 5 @ 0.66787, 10 @ 0.74019 60 Edge Lengths: 20 @ 0.37490, 10 @ 0.59300, 10 @ 0.63224, 10 @ 0.64984, 10 @ 0.84072
GCD is 2.
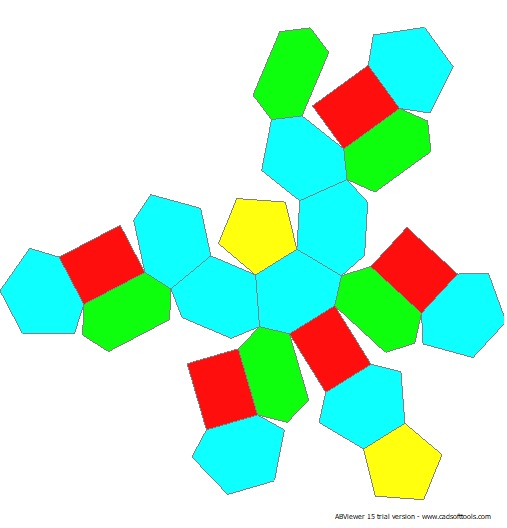 FLAT
FLAT
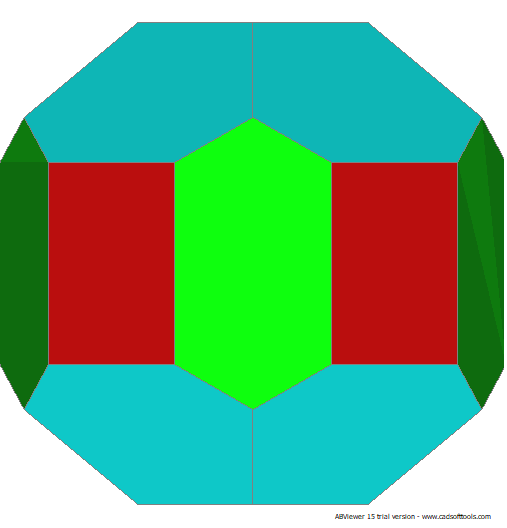 LEFT
LEFT
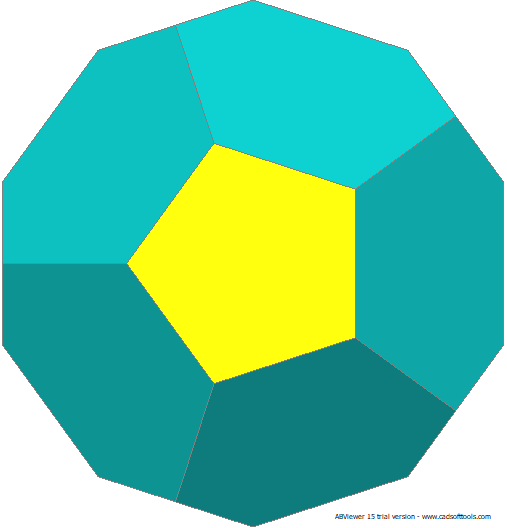 TOP
TOP
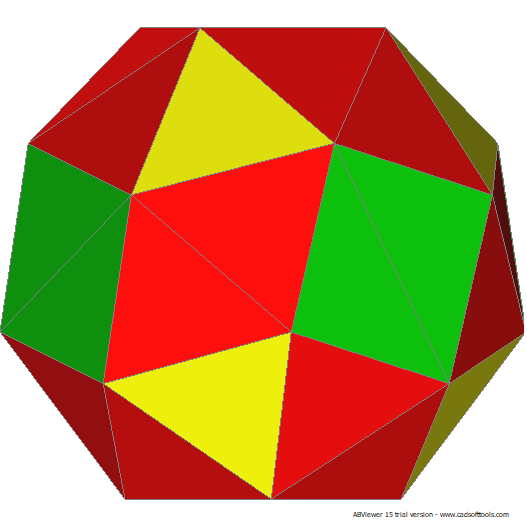
24 hubs: 44 Faces in 3 groups: 24@0.24552, 8@0.25488, 12@0.25614: 66 Edges in 4 groups : 24@0.71573, 24@0.76720, 12@0.78056, 6@1.01217:
This has 6 square faces. the triangular 12@0.25614 are square 6@0.51228:
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
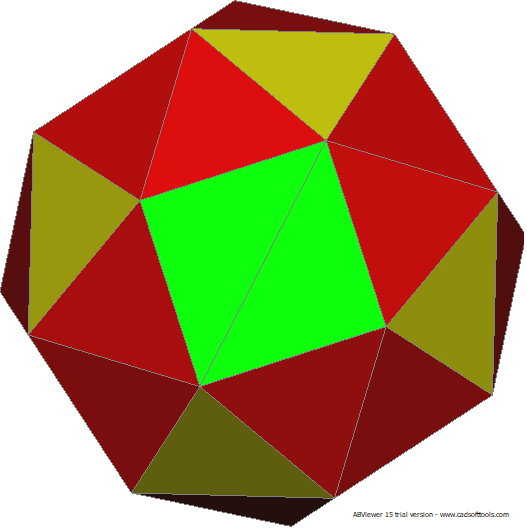
38 Hubs. 32h3 and 6h2: 24 Face Areas: 24@0.59942: 60 Edge Lengths: 12@0.47167, 24@0.51802, 24@0.74170
Note that all faces are identical in size and "arrowhead" shape. Arrowhead is not symmetrical about long axis.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
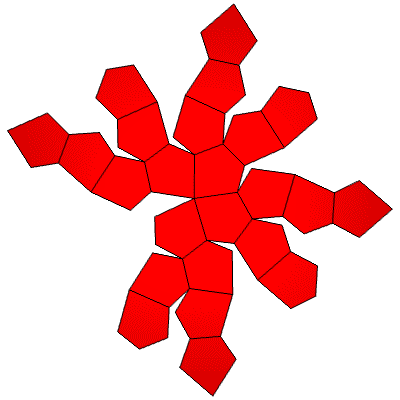
27 Hubs: 50 Faces in 3 group areas: 20@0.21675, 10@0.22627, 20@0.22908: 75 Edges in 6 group lengths: 20@0.68175, 20@0.70053, 10@0.70170, 5@0.72099, 10@0.77245, 10@0.82808.
Rotational 5-part symmetry, and mirror top to bottom.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
50Hub3: 27 Face Areas: 10@0.50332, 2@0.50994, 10@0.53873, 5@0.54225: 75 Edge Lengths: 10@0.29687, 10@0.37422, 5@0.45139, 30@0.54440, 20@0.58603
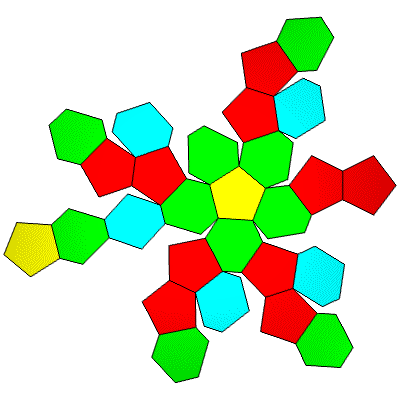 FLAT
FLAT
 LEFT
LEFT
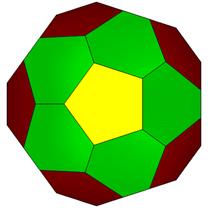 TOP
TOP
28 Hubs. 12h5, 16H6
52 Faces: 12@0.21146, 12@0.21312, 12@0.21409, 12@0.22205, 4@0.22451
78 Edges: 12@0.64688, 6@0.67043, 12@0.67981, 12@ 0.71145, 12@0.71726, 12@0.72005, 12@0.81489,
13:1 tetra
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
 Tetra
Tetra
52Hub3
28 Faces: 12@0.48260, 4@0.50961, 12@0.52174,
78 Edges: 12@0.27405, 12@0.45605, 12@0.46687, 12@0.49064, 6@0.52543, 12@0.54973, 12@0.63605,
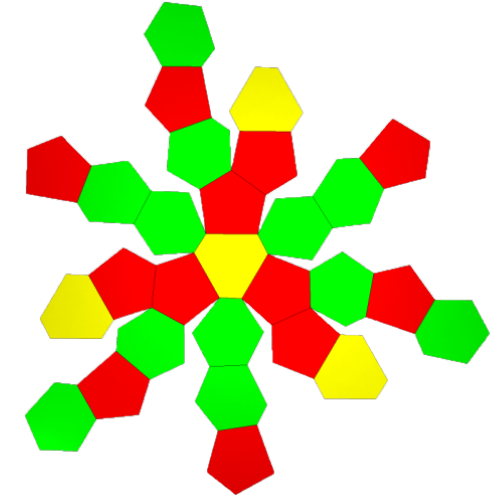 FLAT
FLAT
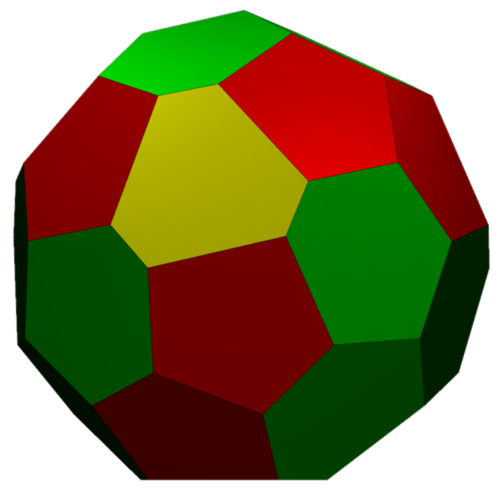 LEFT
LEFT
 TOP
TOP
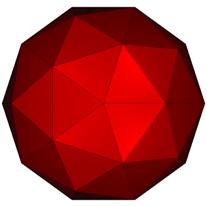
32 Hubs: 60 Faces: 60@0.18995: 90 Edges: 60@0.64085, 30@0.71364
Each dodecahedron face replaced by 5 identical isosceles triangles.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
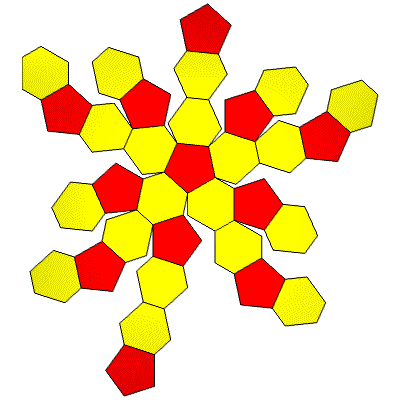
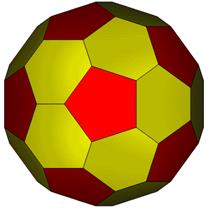
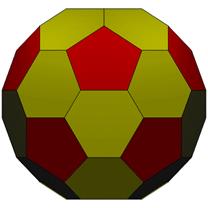
60 Hub3: 32 Face Areas in 2 groups: 12@0.41566, 20@0.44427: 90 Edge Lengths in 2 groups: 30@0.34010, 60@0.49151
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
38 Hubs:
72 Faces: 12@0.15153, 12@0.15939, 12@0.15939, 12@0.16335, 12@0.16530, 12@0.16530:
108 Edges: 24@0.56949, 24@0.59042, 12@0.59383,12@0.61738, 12@0.62516, 12@0.63945
 FLAT
FLAT
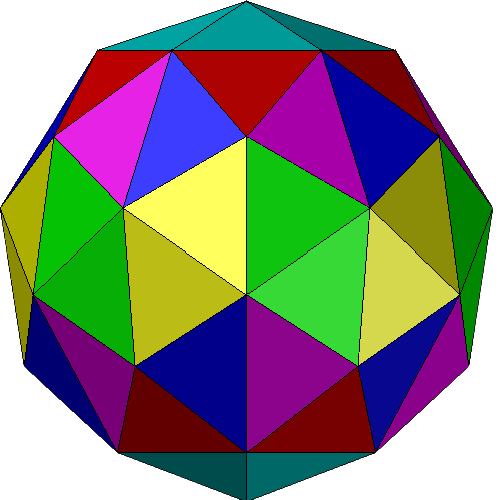 LEFT
LEFT
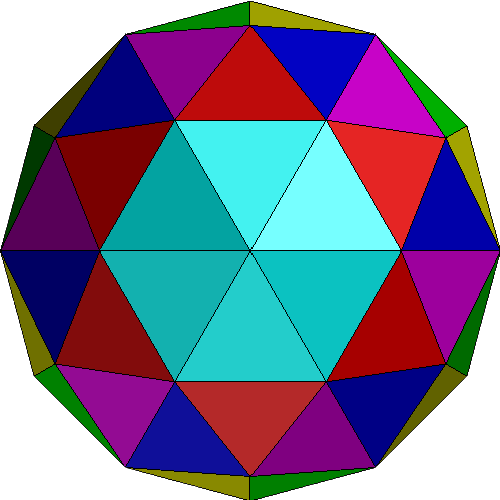 TOP
TOP
72 Hub3:
38 Face Areas in 5 groups: 12@0.34932, 12@0.36226, 6@0.36402, 6@0.36402, 2@0.37649:
108 Edge Lengths in 7 groups: 12@0.15883, 12@0.33617, 12@0.38065, 12@0.38444, 12@0.40569, 24@0.45834, 24@0.50834 .
From dark blue center, a multi-color radial pattern is repeated 6 times.
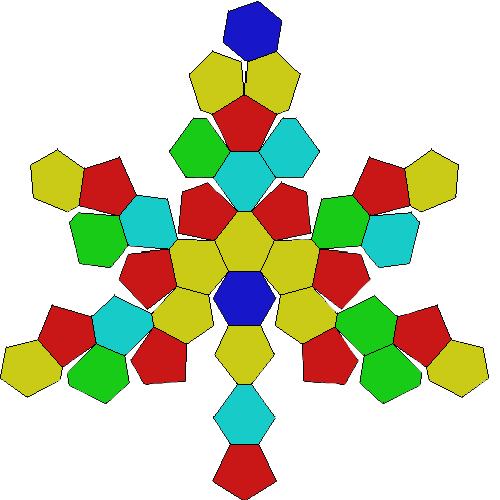 FLAT
FLAT
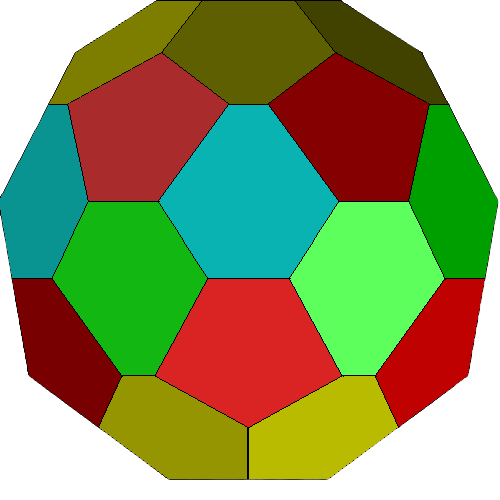 LEFT
LEFT
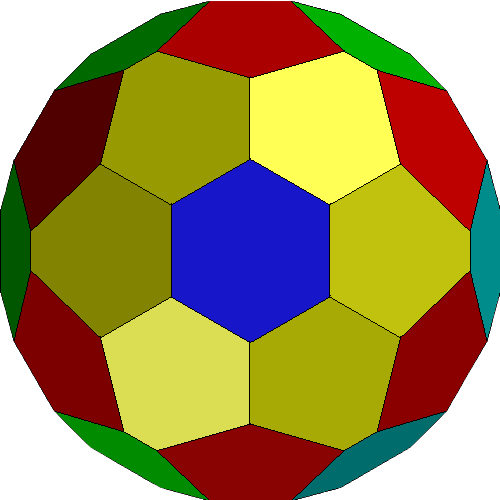 TOP
TOP
38 Hubs:
72 Face Areas: 24 @ 0.13844, 24 @ 0.14902, 24 @ 0.19338:
108 Edge Lengths: 12 @ 0.49923, 24 @ 0.52683, 48 @ 0.64707, 24 @ 0.71873
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
72 Hub3:
38 Face Areas: 6 @ 0.29824, 24 @ 0.35935, 8 @ 0.41086,:
108 Edge Lengths: 24 @ 0.20209, 48 @ 0.40054, 12 @ 0.54322, 24 @ 0.54611
.
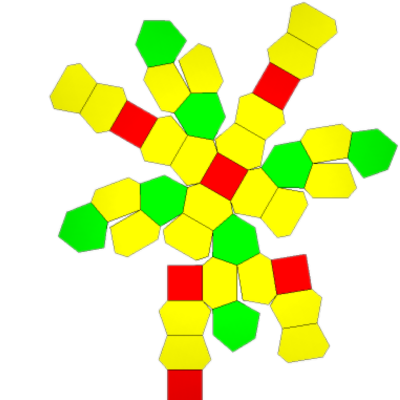 FLAT
FLAT
 LEFT
LEFT
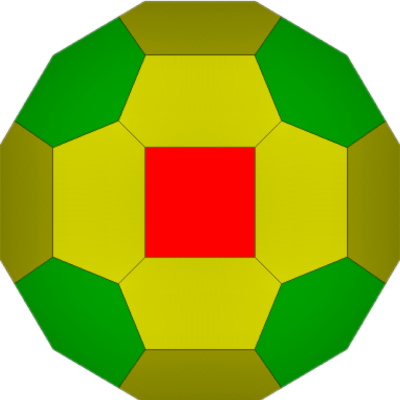 TOP
TOP
40 Hubs-12@5, 28@6: 76 Face Areas: 12 @ 0.14641, 24 @ 0.15154, 24 @ 0.15210, 12 @ 0.15865, 4 @ 0.16889 114 Edge Lengths: 12 @ 0.54987, 6 @ 0.55878, 24 @ 0.56333, 24 @ 0.58517, 12 @ 0.62452, 24 @ 0.63285, 12 @ 0.65956
19::1 Tetrahedron symmetry. Both of the 24-element face groups have half/half mirror images
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
76 Hub3: 40 Face Areas: 12 @ 0.32017, 4 @ 0.33908, 12 @ 0.34946, 12 @ 0.35038: 114 Edge Lengths: 12 @ 0.25699, 24 @ 0.32734, 12 @ 0.34937, 24 @ 0.41377, 24 @ 0.42726, 12 @ 0.47655, 6 @ 0.47900:
10:1 Tetrahedron symmetry.
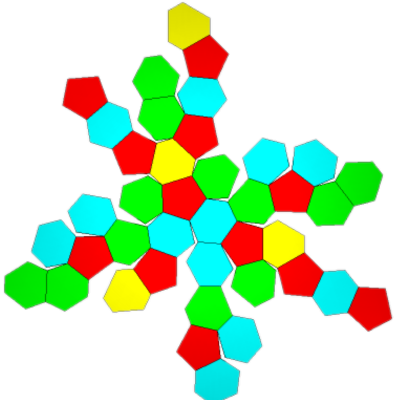 FLAT
FLAT
 LEFT
LEFT
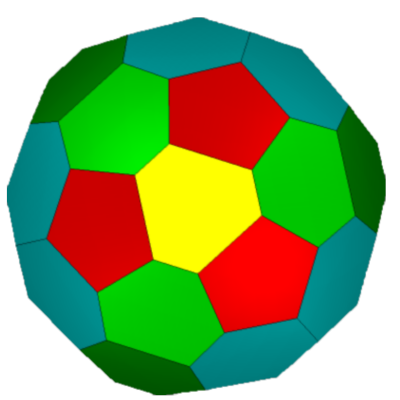 TOP
TOP
Hubs( 12@5, 30@6 ) 80 Faces in 2 groups: 60@0.13930, 20@0.16540 GCD=20. 120 Edges in 2 groups: 60@0.54653, 60@0.61803
Looking at the left side view, notice the bottom half could be rotated 36 degrees and still have a valid Geodesic. Curious.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
80@Hub3: 42 Face Areas: 12@0.29316, 30@0.33428: 120 Edge Lengths: 60@0.33395, 60@0.41279,
7::1 Cube. 2 red &5 yellow
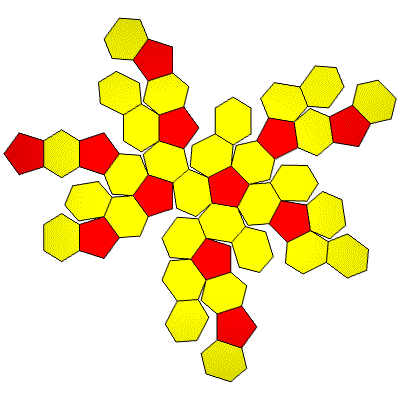 FLAT
FLAT
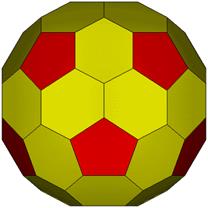 LEFT
LEFT
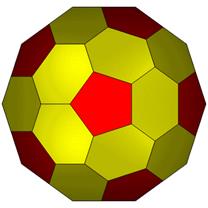 TOP
TOP
44 Hubs: 78 Faces in three groups: 24@0.13168, 48@0.14177, 6@0.29040: 120 Edges in 4 groups: 24@0.53888, 24@0.55692, 48@0.55805, 24@0.60580
14:1 breakdown of a cube (count square as two triangles). Has square openings.
This is a great shape to use for a cubby house or tree house. 6 square openings equally spaced make natural windows or door opening. A square floor fits in easily. Internal poles which follow the original cube edges are natural for curtains, or counter top edges, etc.
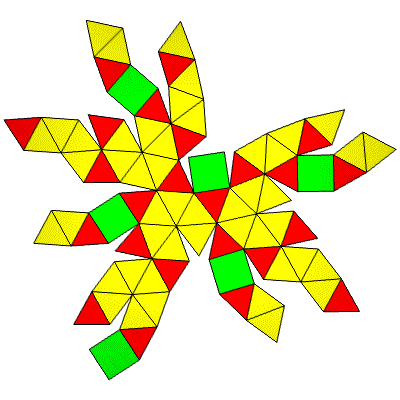 FLAT
FLAT
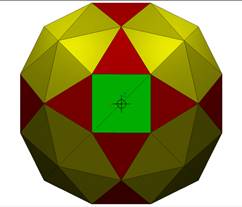 ALL
ALL
72 Hub3 and 6 Hub4. 44 Face Areas: 24@0.30152, 12@0.30985, 8@0.31787: 120 Edge Lengths: 24@0.30254, 48@0.36768, 24@0.39922, 24@0.48891,
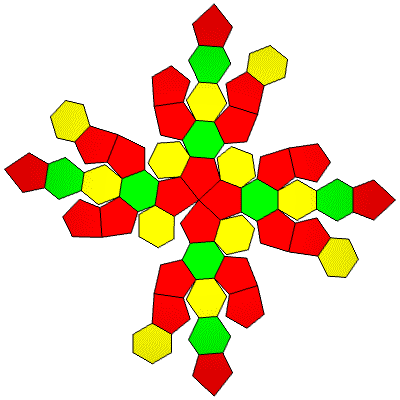 FLAT
FLAT
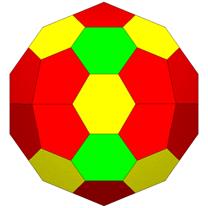 LEFT
LEFT
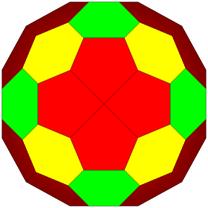 TOP
TOP
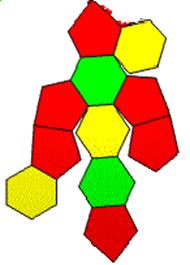
46Hubs: 88 Face Areas in 7 groups: 12@0.12779, 12@0.13081, 16@0.13182, 12@0.13231, 12@0.13527, 12@0.13798, 12@0.13866 GCD is 4. 132 Edge Lengths in 9 groups: 24@0.51460, 24@0.53247, 12@0.53309, 12@0.54648, 12@0.55172, 12@0.57299, 12@0.59810, 12@0.62066, 12@0.63568,
22:1 tetra breakdown, maybe.
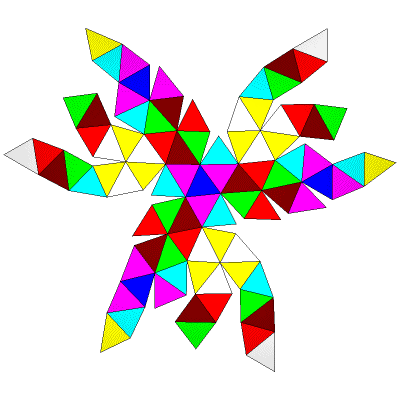 FLAT
FLAT
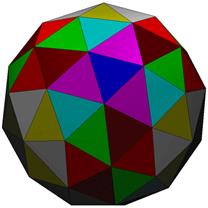 LEFT
LEFT
 TOP
TOP

96 Hub3: 46 Face Areas in 5 groups: 12@0.27780, 6@0.29324, 4@0.29504, 12@0.29849, 12@0.30007: 132 Edge Lengths in 11 groups: 12@0.21169, 12@0.23788,12@0.27299, 12@0.32988, 12@0.36413, 12@0.38440, 12@0.40274, 12@0.41106, 12@0.42427, 12@0.42574, 12@0.44692:
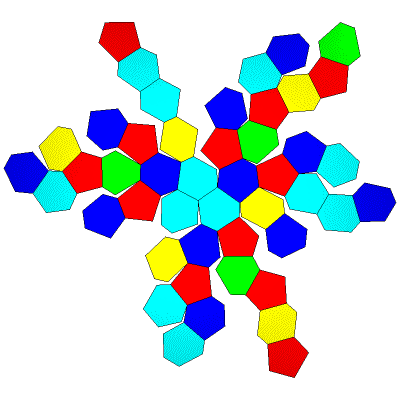 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
48Hubs.
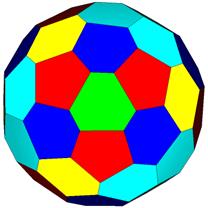
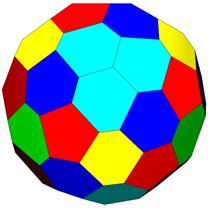
92 Face Areas in 5 groups: 24@0.12363, 24@0.12691,24@0.13055, 12@0.13124, 8@0.13213 GCD = 4.
138 Edge Lengths in 7 groups: 24@0.51232, 24@0.51865, 24@0.53793, 24@0.55236, 24@0.55527, 12@0.60130, 6@0.72440,
12@0.13124 triangles are 6@0.26248 squares. Tetra breakdown would be 23::1
 FLAT
FLAT
 LEFT
LEFT
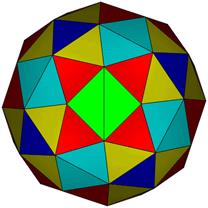 TOP
TOP
86 Hubs.
48 Face Areas in 2 groups: 24@0.27392, 24@0.28502: GCD=24.
132 Edge Lengths in 6 groups: 12@0.25082, 24@0.30902, 24@0.33730, 24@0.35982, 24@0.39928, 24@0.47317,
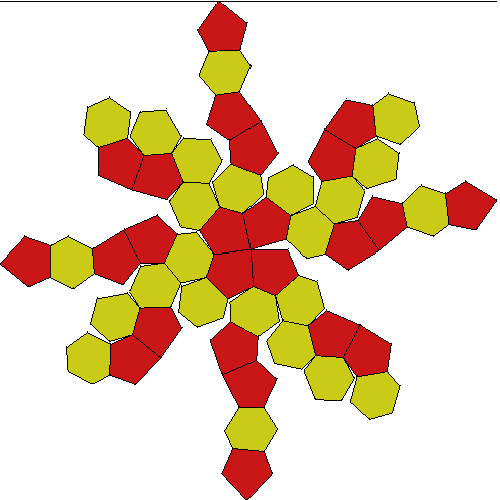 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
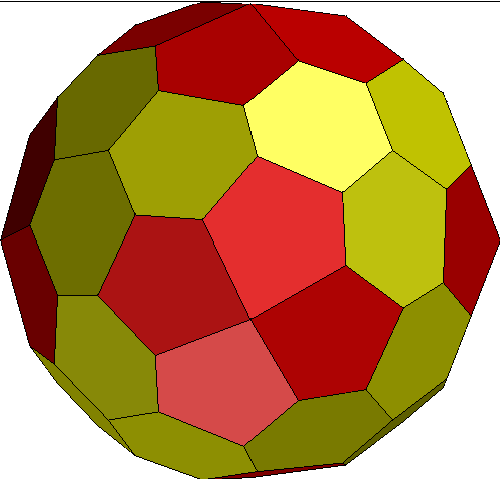
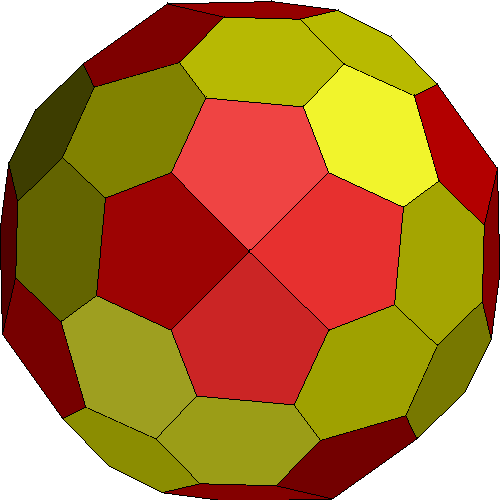
50Hubs. 96 Faces in 5 groups: 12@0.11694, 24@0.12029, 24@0.12512,12@0.12519,24@0.12557: GCD=12. 144 Edges in 9 groups: 12@0.49310, 24@0.50442, 12@0.51260, 24@0.51746, 12@0.52422, 12@0.54482, 12@0.55645, 24@0.57245, 12@0.61645
Six-part rotational symmetry. Possible 2, tetra, cube, and dodeca breakdowns.
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
96 Hub3. 50 Face Areas in 5 groups: 12@0.25453, 12@0.26964, 12@0.27027, 12@0.27418, 2@0.27767: GCD=2. 144 Edge Lengths in 9 groups:12@0.19362, 24@0.26509, 12@0.31840, 12@0.32690, 12@0.34063, 12@0.36993, 24@0.37136, 24@0.40672, 12@0.42206
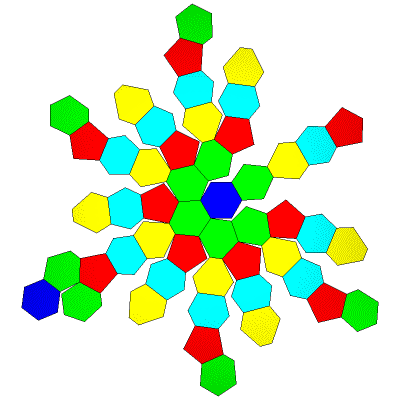 FLAT
FLAT
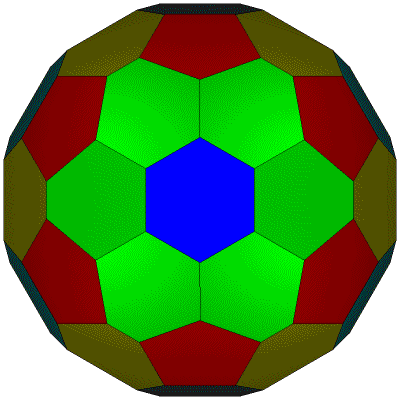 LEFT
LEFT
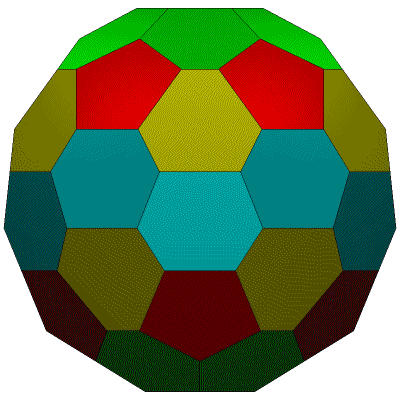 TOP
TOP
72 Hubs. 140 Faces: 20@0.08382, 60@0.08486,60@0.08786: GCD=20. Possible tetra(4), icosa(20) breakdowns. 210 Edges: 60@0.42482, 30@0.43008, 60@0.43998, 60@0.48801
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
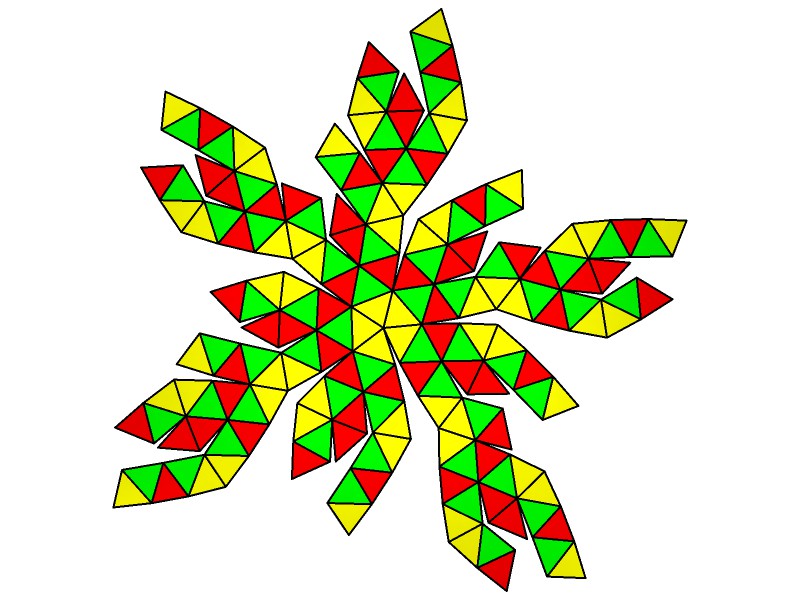
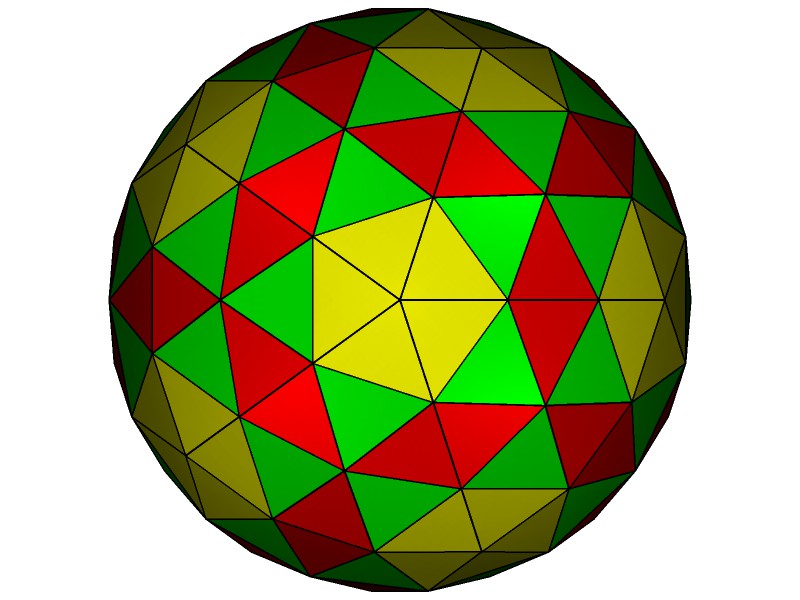
140 Hub3: 72 Face Areas in 2 groups: 12@0.17165, 60@0.18433: GCD=12. 210 Edge Lengths in 4 groups: 60@0.19840, 60@0.28725, 60@0.31583, 30@0.32046,
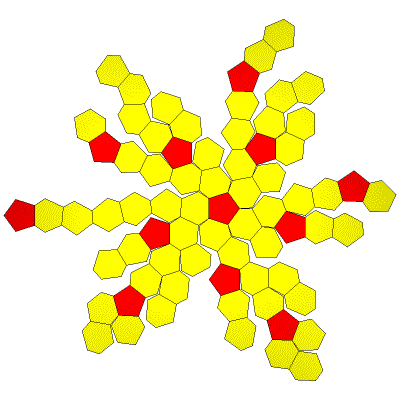 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
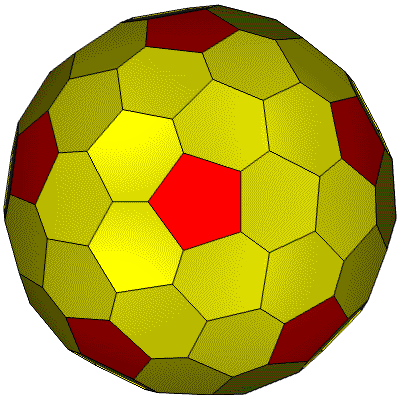
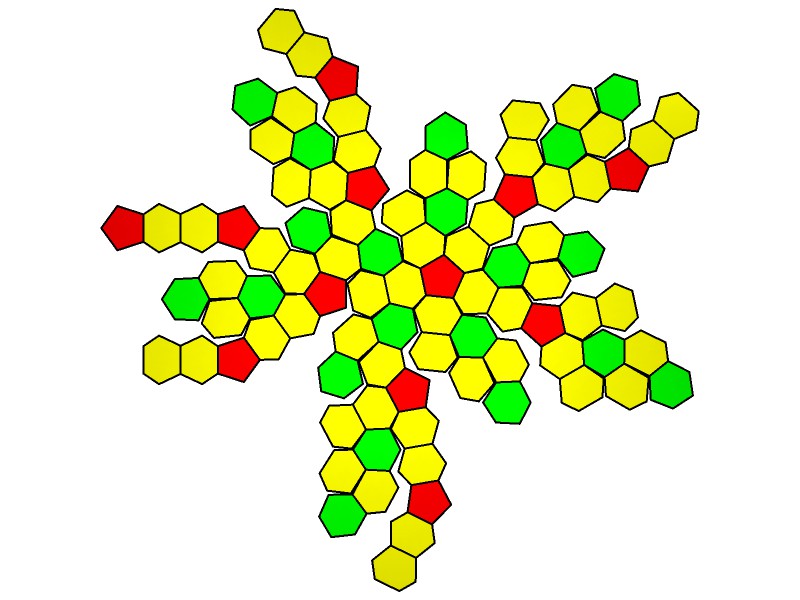
92 Hubs. 180 Faces in 3 groups: 60@0.06462, 60@0.06493, 60@0.07300: GCD=60. 270 Edges in 4 groups: 30@0.36050, 60@0.37018, 120@0.40281, 60@0.42766
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
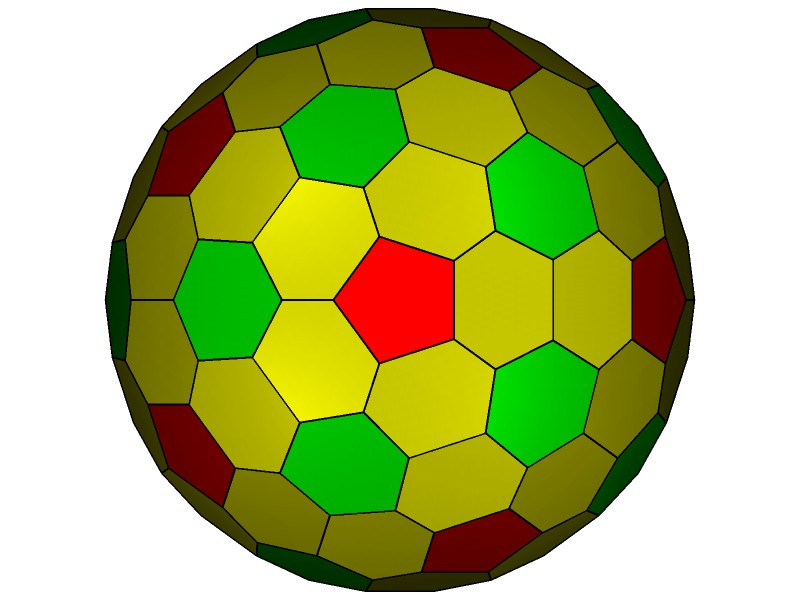
180 points 92 Face Areas: 12@0.12887, 60@0.14185, 20@0.14693: GCD=4. 270 Edge Lengths: 60@0.18859, 120@0.23819, 60@0.27368, 30@0.28177
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
122 Hubs. 240 Face Areas in 4 groups: 60@0.04964, 60@0.05061R, 60@0.05061L, 60@0.05339: GCD=60. 360 Edge Lengths in 5 groups: 60@0.32413, 60@0.32534,120@0.34057, 60@0.36284, 60@0.37601
 FLAT
FLAT
 LEFT
LEFT
 TOP
TOP
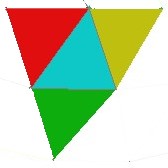
The face index color is set by face size and shape groups. Red is index 1, used for the smallest triangle. Yellow is index 2. Green is index 3. And so on. The color black is used for lines by the system, so not used here for face color. Many spheres with too many different triangle shapes and sizes are assumed to be difficult to work with, and are not in this book.
DXF color
PenToColorMapEntry_t( 0, RGB( 255, 255, 255 ) ), black(not used)
PenToColorMapEntry_t( 1, RGB( 255, 0, 0 ) ), red. Usually the smallest face.
PenToColorMapEntry_t( 2, RGB( 255, 255, 0 ) ), yellow. Next smallest face.
PenToColorMapEntry_t( 3, RGB( 0, 255, 0 ) ), green
PenToColorMapEntry_t( 4, RGB( 0, 255, 255 ) ), aqua or light blue
PenToColorMapEntry_t( 5, RGB( 0, 0, 255 ) ), blue
PenToColorMapEntry_t( 6, RGB( 255, 0, 255 ) ), purple
PenToColorMapEntry_t( 7, RGB( 0, 0, 0 ) ), white
PenToColorMapEntry_t( 8, RGB( 128, 128, 128 ) ), grey
PenToColorMapEntry_t( 9, RGB( 190, 190, 190 ) ), light grey